Библиотека Python NumPy

Python широко известен в среде DataScience, человек однажды применивший технологии языка для проведения математического или аналитического исследования однозначно не сможет представить свою работу без него. Большинство людей знают, что Python мощный, но некоторые обеспокоены его низкой производительностью при решении высокопроизводительных инженерных задач. В этой статье мы рассмотрим потенциал Python и NumPy.

Почему именно Python?

Это правда, что Python, как интерпретируемый язык, работает намного медленнее, чем компилируемые языки, такие как C, C++, Java и т.д. Программы, написанные на интерпретируемых языках, не выполняются непосредственно процессором. Интерпретатор анализирует исходный код Python, преобразует его в простой формат (байт-код), затем последовательно выполняет байт-код строка за строкой. Python динамически типизирован, где переменными могут быть объекты любого типа. Хотя интерпретация и динамическая типизация делают Python медленным при работе с интенсивной нагрузкой на процессор, эти функции делают Python удобным для пользователя и гибким при программировании и работе со сложными структурами данных. Программистам, которые перешли с C++ или Java на Python у вас вероятно будет не привычно, поскольку Java статически и компилируемо типизирован. Постепенно привыкнув, можно заметить, что Python проще из-за удобного для чтения синтаксиса и более гибок из-за отсутствия объявления типа данных переменных.

CPython

Возможно, вы слышали о CPython, который является стандартным интерпретатором Python, написанным на C, который переводит и запускает программы на Python. CPython использует скорость C и может быть удобно использован в Python. Существуют модули Python, такие как math, pandas, NumPy или SciPy, которые в значительной степени основаны на C. В Python мы назвали эти модули расширениями, которые расширяют функциональность Python, реализуя код на таких языках, как C или C++. Возможно, вы уже видели файл .so в Linux или файл .pyd в Windows, эти файлы представляют собой скомпилированные библиотеки C или C++, которые можно импортировать как обычные модули Python. Например, в NumPy есть функция load_library для загрузки библиотек C, таких как модули расширения multiarray и umath c.

Эти модули устраняют разрыв между высокоуровневым интерпретируемым кодом Python и низкоуровневым быстро компилируемым кодом для повышения производительности при выполнении задач, требующих больших вычислительных затрат. Работая над разработкой графического интерфейса, я узнал, что PyQt/ PySide также являются модулями расширения Python, поскольку большинство их кодов реализовано на C/C++ с использованием Qt framework, которая также написана на C++. Я нахожу удобным использовать PyQt / PySide для разработки графического интерфейса, поскольку я могу получить доступ к функциональным возможностям C++ через привязки Python, что упрощает процесс разработки графического интерфейса.

NumPy

Numerical Python (NumPy) - один из самых фундаментальных пакетов для численных вычислений на Python. Он предоставляет память и эффективные для вычислений многомерные массивы (ndarray), а также богатый набор функций.

Массивы NumPy в сравнении со списками Python

Списки Python и массивы NumPy - это две популярные структуры данных Python для хранения элементов, но у них есть некоторые различия. Изначально я думал, что списки Python более просты в хранении элементов и управлении ими, чем массивы NumPy. Когда я начал работать с очень большими наборами данных, я понял, что списки Python не являются идеальной структурой данных, особенно для числовых данных.

Списки Python основаны на массивах указателей на объекты, хранящихся в памяти. Указатели в массиве не хранят данные объекта напрямую; они указывают на область памяти, где находятся данные объекта. Массивы NumPy хранят элементы последовательно в памяти вместе с необходимыми метаданными (форма массива, размер, тип данных и т.д.) для отслеживания структуры.

Если вам нужно выполнить много числовой обработки данных и вычислений, NumPy должен быть вашим вариантом структуры данных, поскольку он может выполнять арифметические операции без написания каких-либо явных циклов (векторизация).

Векторизация

Вместо итерации по каждому элементу массива, векторизация в NumPy выполняет поэлементные операции одновременно без использования цикла for.

In [12]: from random import randint

In [13]: N = 500000

In [14]: %timeit samples = [randint(0, 50) for in range(N)]
220 ms ± 5.93 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [15]: %timeit np.random.randint(N)
2.09 μs ± 150 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

Векторизованный подход значительно быстрее, чем циклами. Еще одна возможность NumPy, которая имеет отношение к векторизованным вычислениям, называется трансляцией (broadcasting).

Broadcasting (трансляция)

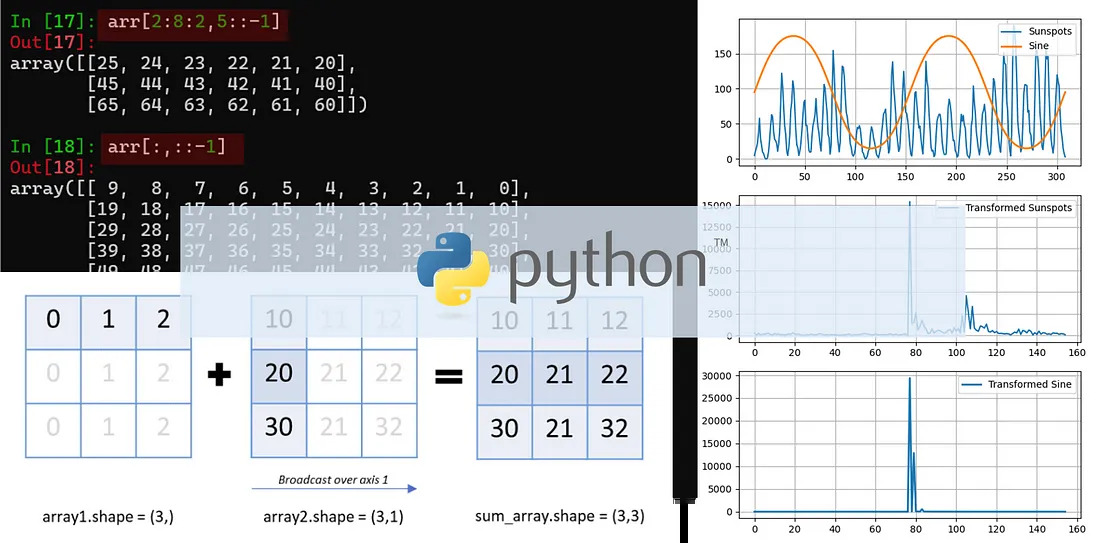
Трансляция - это операция, позволяющая выполнять арифметические действия с массивами различной формы.

In [24]: import numpy as np

In [25]: array1 = np.arange(3)

In [26]: array1
Out[26]: array([0, 1, 2])

In [27]: array2 = np.array([[10], [20], [30]])

In [28]: array2
Out[28]: array([[10], [20], [30]])

In [29]: sum_array = array1 + array2

In [30]: sum_array
Out[30]: array([[10, 11, 12], [20, 21, 22], [30, 31, 32]])

В операции сложения одномерный массив (array1) преобразуется в формат двухмерного массива (array2). array1 (3,) реплицируется вдоль столбца и становится массивом (3,1).

Мне всегда приходится ломать голову, когда речь заходит о представлении работы трансляции, и вот наглядный способ (вдохновленный книгой Уэса Маккинни) понять трансляцию по оси 0 или 1 двумерного массива.

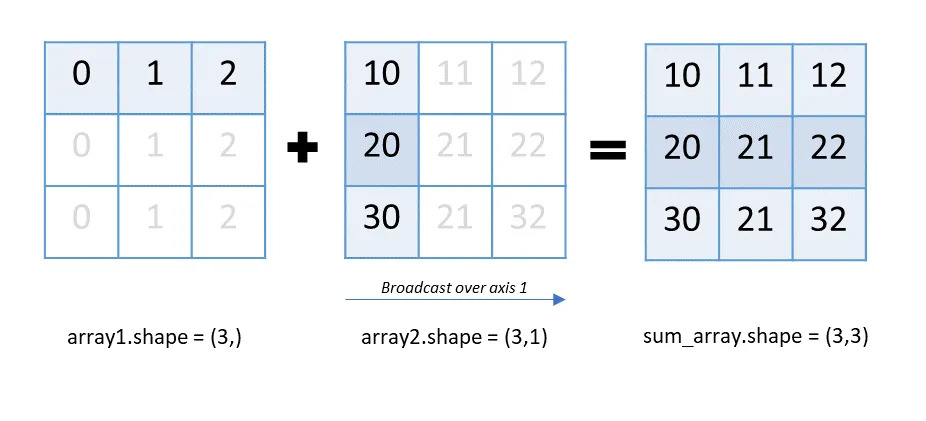
Ниже приведен пример трансляции по оси 0:

In [78]: import numpy as np

In [79]: array1 = np.random.randint(0, 10, size=(2, 4, 2))

In [80]: array1
Out [80]: array([[[9, 8], [6, 7], [2, 5], [4, 9]], [[2, 1], [0, 4], [8, 3], [9, 4]]])

In [81]: array1.shape Out [81]: (2, 4, 2)

In [82]: array2 = np.random.randint(0, 10, size=(4, 2))

In [83]: array2
Out [83]: array([[5, 5], [2, 0], [6, 3], [5, 9]])

In [84]: array2.shape
Out[84]: (4, 2)

In [85]: sum_array = array1 + array2

In [86]: sum_array
Out [86]: array([[[14, 13], [ 8, 7], [ 8, 8], [ 9, 18]], [[ 7, 6], [ 2, 4], [14, 6], [14, 13]]])

In [87]: sum_array.shape
Out[87]: (2, 4, 2)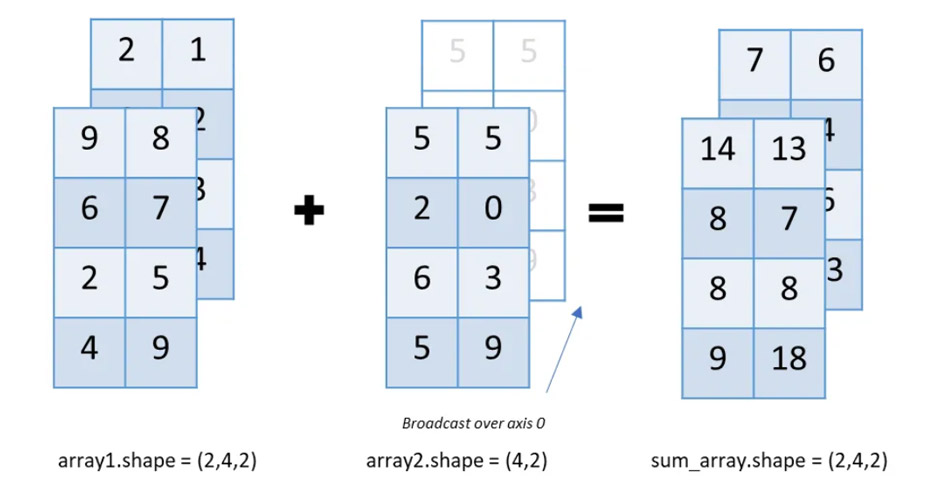

Reshape, переформатирование или изменение формы

Бывали случаи, когда я изменял форму массивов ndarrays, чтобы создать желаемые формы массивов для обработки и визуализации данных. Иногда нам приходится изменять форму массивов, когда одна из используемых библиотек Python ожидает определенный формат данных. Функция numpy.reshape в NumPy изменяет расположение массива данных без изменения или копирования каких-либо данных.

In [2]: import numpy as np

In [3]: arr = np.arange(6)

In [4]: arr
Out [4]: array([0, 1, 2, 3, 4, 5])

In [5]: arr.reshape((3,2))
Out [5]: array([[0, 1], [2, 3], [4, 5]])

In [6]: arr.reshape((2,3))
Out [6]: array([[0, 1, 2], [3, 4, 5]])

Согласно документации, при указании новой фигуры один размер фигуры может быть равен -1, значение которого, используемое для этого, будет выведено из длины массива.

In [7]: arr.reshape((3,-1))
Out [7]: array([[0, 1], [2, 3], [4, 5]])

In [8]: arr.reshape((-1,3))
Out [8]: array([[0, 1, 2], [3, 4, 511)

Ravel vs Flatten

Чтобы свести все элементы в одну строку, мы можем использовать ravel и flatten в NumPy. Мы часто выравниваем массивы, когда алгоритм или библиотека визуализации ожидает одномерные данные.

In [3]: arr1 = arr.reshape((3,2))
In [4]: arr1
Out [4]: array([[0, 1], [2, 3], [4, 5]])

In [5]: arr1.ravel()
Out [5]: array([0, 1, 2, 3, 4, 5])

In [6]: arr1.flatten()
Out [6]: array([0, 1, 2, 3, 4, 5])

Ravel часто работает быстрее, чем flatten, особенно для больших массивов, поскольку ravel не копирует данные, в то время как при сглаживании массива возвращается копия массива данных. Изменение массива ravel может привести к изменению исходного массива, поскольку функция ravel создает представление того же массива.

Индексация и срез массивов

Индексация массива и срез в NumPy - это два метода эффективного извлечения элементов без копирования данных (за исключением сложной индексации).

In [13]: arr = np.arange(10*10).reshape(10,10)

In [14]: arr
Out [14]: array([[0,  1, 2, 3, 4, 5, 6, 7 8, 9],
[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
[20, 21 22, 23, 24, 25, 26, 27, 28, 29],
[30, 31 32, 33, 34, 35, 36, 37, 38, 39],
[40, 41 42, 43, 44, 45, 46, 47 48, 49],
[50, 51, 52, 53, 56, 57, 58, 59],
[60, 61, 62, 63, 64, 65 66, 67 68, 69],
[70, 71, 72, 73, 74, 75 76, 77, 78, 79],
[80, 81, 82, 83, 84, 85, 86, 87, 88, 89],
[90, 91, 92, 93, 94, 95, 96, 97, 98, 99]])

In [15]: arr[2: 8: 2, :]
Out [15]: array([[20, 21 22, 23, 24, 25, 26, 27, 28, 29],
[40, 41 42, 43, 44, 45, 46, 47 48, 49],
[60, 61, 62, 63, 64, 65 66, 67 68, 69]])

In [16]: arr[2: 8: 2, 5:]
Out [16]: array([[25, 26, 27, 28, 29],
[45, 46, 47, 48, 49],
[65, 66, 67, 68, 69]])

Обозначение для среза. [start_index : end_index : steps]. start_index включен в выборку, а end_index исключен.

In [17]: arr[2: 8: 2, 5 : : -1]
Out [17]: array([[25, 24, 23, 22, 21, 20],
[45, 44, 43, 42, 41, 40],
[65, 64, 63, 62, 61, 60]])

In [18]: arr[:, : :-1]
Out [18]: array([[9, 8, 7, 6, 5, 4, 3, 2, 1, 0],
[19, 18, 17, 16, 15, 14, 13, 12, 11, 10],
[29, 28, 27, 26, 25, 24, 23, 22, 21, 20],
[39, 38, 37, 36, 35, 34, 33, 32, 31, 30],
[49, 48, 47, 46, 45, 44, 43, 42, 41, 40],
[59, 58, 57, 56, 55, 54, 53, 52, 51, 50],
[69, 68, 67, 66, 65, 64, 63, 62, 61, 60],
[79, 78, 77, 76, 75, 74, 73, 72, 71, 70],
[89, 88, 87, 86, 85, 84, 83, 82, 81, 80],
[99, 98, 97, 96, 95, 94, 93, 92, 91, 90]])

arr[ : : -1] или arr[ :, : : -1] подсчитывает индексы в обратном порядке и возвращает список в обратном порядке.

In [25]: arr[-1:,:]
Out [25]: array([[90, 91, 92, 93, 94, 95, 96, 97, 98, 99]])

In [26]: arr[-1:,:-1]
Out [26]: array([[90, 91, 92, 93, 94, 95, 96, 97, 98]])

arr[-1:,:] устанавливает значение start_index равным -1 для строки, которая выбирает последнюю строку. arr[-1: ,:-1] выбирает все элементы в последней строке, за исключением последнего элемента в этой строке.

In [47]: row_index = (arr[:, 0]>=30) & (arr[:,0]<=70)

In [48]: col_index = arr[0,:]>=5

In [49]: row_index
Out [49]: array([False, False, False, True, True, True, True, True, False, False])

In [50]: col_index
Out [50]: array([False, False, False, False, False, True, True, True, True, True])

In [51]: arr[row_index, :] [:, col_index]
Out [51]: array([[35, 36, 37, 38, 39],
[45, 46, 47, 48, 49],
[55, 56, 57, 58 59],
[65, 66, 67, 68, 69],
[75, 76, 77, 78, 79]])

Логическая индексация в массиве NumPy

Индексация и разбиение массива на части в NumPy часто используются для выбора элементов массива данных и манипулирования ими. Помимо этих функций, существуют другие процедуры NumPy для манипулирования массивом, которые можно найти в их документации. NumPy также предлагает полный набор математических процедур, таких как операции линейной алгебры, численная оптимизация и быстрое преобразование Фурье.

Быстрое преобразование Фурье

При обработке сигналов быстрое преобразование Фурье (FFT) имеет решающее значение для анализа и обработки сигналов путем преобразования их во временной области (амплитуда зависит от времени) и частотной области (амплитуда зависит от частоты).

Анализ Фурье

import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

data_loader = sm.datasets.sunspots.load_pandas()
sunspots = data_loader.data["SUNACTIVITY"].values

t = np.linspace(-2 * np.pi, 2 * np.pi, len(sunspots))
mid = np.ptp(sunspots)/2
sine = mid + mid * np.sin(np.sin(t))

sine_fft = np.abs(np.fft.fftshift(np.fft.rfft(sine)))
print("Index of max sine FFT", np.argsort(sine_fft)[-5:])

transformed = np.abs(np.fft.fftshift(np.fft.rfft(sunspots)))
print("Indices of max sunspots FFT", np.argsort(transformed)[-5:])

plt.subplot(311)
plt.plot(sunspots, label="Sunspots")
plt.plot(sine, lw=2, label="Sine")
plt.grid(True)
plt.legend()
plt.subplot(312)
plt.plot(transformed, label="Transformed Sunspots")
plt.grid(True)
plt.legend()
plt.subplot(313)
plt.plot(sine_fft, lw=2, label="Transformed Sine")
plt.grid(True)
plt.legend()
plt.show()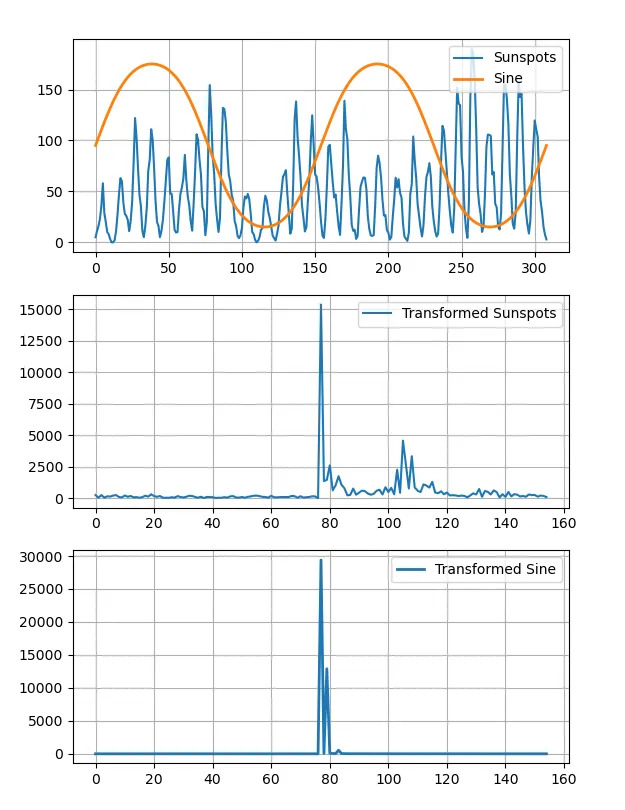

Как показано в приведенном выше коде, при выполнении БПФ для сигнала результат БПФ является сложным, поскольку он представляет информацию как об амплитуде (действительная часть - величина), так и о фазе (мнимая часть) частотных составляющих сигнала. Поэтому мы используем np.abs() для извлечения величины спектра из комплексного результата БПФ.

Спектральный анализ

import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

data_loader = sm.datasets.sunspots.load_pandas()
sunspots = data_loader.data["SUNACTIVITY"].values

transformed = np.fft.fftshift(np.fft.rfft(sunspots))

plt.subplot(311)
plt.plot(sunspots, label="Sunspots")
plt.legend()
plt.subplot(312)
plt.plot(transformed ** 2, label="Power Spectrum")
plt.legend()
plt.subplot(313)
plt.plot(np.angle(transformed), label="Phase Spectrum")
plt.grid(True)
plt.legend()
plt.show()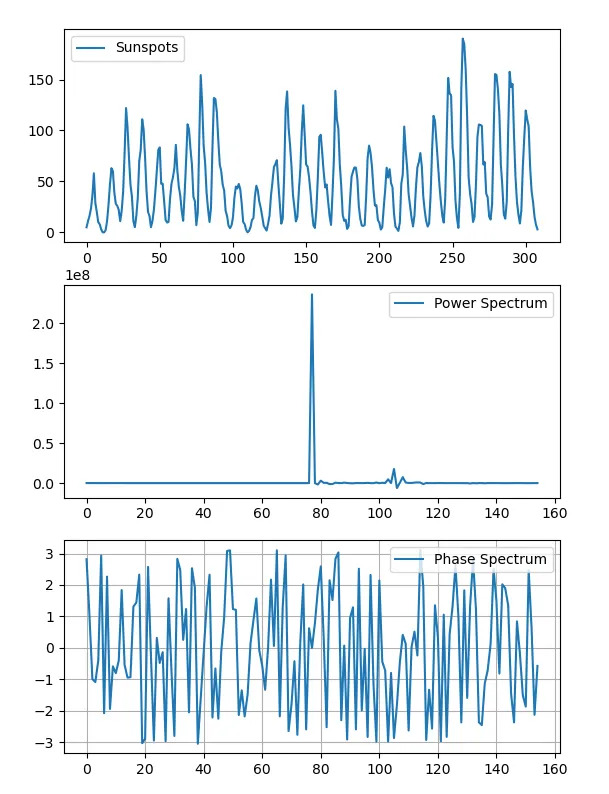

Как правило, мы часто применяем БПФ при работе со спектральными данными для частотного анализа (для определения основных частот, присутствующих в сигнале), фильтрации (для выбора, изменения или удаления определенных частот), модуляции сигнала и демодуляции в системах связи.

Заключение

Этот пост в блоге представляет собой компиляцию некоторых фундаментальных концепций и практических применений Python и NumPy, которые я изучил на работе и в прошлых проектах. Однако этот пост лишь коснулся поверхности. По мере углубления вы откроете для себя обширную коллекцию функций, библиотек и приемов Python и NumPy, которые подходят для вашего конкретного случая использования. Чем больше вы будете изучать, тем больше узнаете.